

我々はここまで、コインの資産価値推移に関して
・定量的且つ客観的情報をどのように見つけ収集するのか
・その情報が持つ弱点となり得る不都合をどのように補完するのか
・この2つの情報をどのような優先度付けで扱いながら統合していくか
・そもそもコインの価値の源泉は何に起因し、それに照らし合わせて用意した情報をどのように解釈・処理すべきか
について考えてきました。
これらのステップを通じて、コイン1枚1枚の資産価値とその推移について包括的な炙り出すことができたと思います。
そしてこのような手法を実践しているなかで、私は『実質貨幣学的価値』の推移データがある興味深い特徴を持っていることに気が付いたというところで前回の文章を締めくくりました。
その興味深い特徴とは、『弱定常性』です。
弱定常性とは、時系列データの基本的な統計量が時間に依存せず一定であるという統計学的に重要な性質を指します。より具体的には、ある時系列データに対して
・期待値(平均)が一定であること
・分散(データの散らばり度合)が一定であること
・自己共分散(データが時間をおいても自分自身とどれだけ似ているかを表す指標)が、観測時点ではなく『時刻差』にのみに依存して一定であること
という3つの性質を満たす場合に、それは弱定常的な時系列データと呼ばれます。
時系列データがこの性質を満たしていると、統計学的なモデル推定の安定性が向上したり、その予測精度が向上したりと、データ分析者にとって『扱い易い』ものとなり、一般的に好ましい状態であると考えられます。
なんのこっちゃって話ですね。貨幣学の話に一切関係なさそう。
ところがどっこい。
先ほども少し言及したように、これまで紹介してきたStep1 から Step4 までのコインの資産価値に関わる情報の取得と処理に関する丁寧な精神性とその実装をすることにより、『実質貨幣学的価値』の推移データがこの『弱定常性』を満たすことが殊の外多く、そうでない場合でも、複雑ではない操作でそれに限りなく近づけられるケースが殆どであることが、数百枚のコインの資産価値分析の中で見えてきました。
即ち、コインに関する定量データを丁寧に扱えさえすれば(まあそれをできている人間がいないのが業界にいないのが現状なのですが)、少なくとも論理的には、そのコインが近い将来どのような資産価値の推移を辿っていくかをそこそこの精度で安定的に推定できるということになります。
もちろんこれは色々なニュアンスを端折りに端折った言い方になり、話はそんなに単純ではありません。
まず、時系列分析モデルを作るにあたって、どれだけ丁寧にデータを扱うにしても40件程は最低限のデータ数として必要となってきます。普段レポートで私が紹介する資産価値推移のグラフは年次のものになっていますが、実際にはもう少し細かい時間軸のデータを用いることでその壁を乗り越えます。
そしてデータが弱定常性を満たさない場合の処理とモデルの選定も色々細かく考えなければなりません。入力データの数が望まれる量よりも少ない場合、最新鋭の複雑な時系列解析モデルよりも、例えばARIMA(自己回帰和分移動平均モデル)のような伝統的なものの方が分析/予測のパフォーマンスが良くなりがちであることが知られています。
しかしながらARIMA系を含む伝統的な時系列解析モデルの多くは弱定常性を満たさないデータを食べると推定誤差がいたずらに膨らんだり、過剰適合(オーバーフィッティング)のリスクが増したりと、色々と好ましくないことが生じるので、最初から弱定常性を満たすデータを用意するか、難しい場合は満たさないデータを満たすように加工するといったテクニックが必要となります。
例えば先ほどのARIMAを用いる場合、p, d, qという3つのパラメータの指定を通じてモデルが組まれます。
・pは入力データに対して、現在の値を何期前までの値を使って説明しようとするかを指定したパラメータ。
・qは時系列データのノイズの連続を考えた時に、現在の値を何期前までの誤差を用いて説明しようとするかを指定するパラメータ。
・dはdifferenceから来ている名で、元の入力データに対して何回差分を取るかを指定するパラメータ。
dは少し分かりづらいですが、データが定常ではない場合でも、データの絶対値ではなく『増え方/減り方』のみに着目するとそのパターンが定常であることがしばしばあり、『差分のモデル』を考えることで元のデータを上手にモデリングしやすくなるため、AR(pを使う)モデルとMA(qを使う)モデルの橋渡しとして使われます。先述の『加工するといったテクニック』の一例ですね。
しかしどのdの値を取ればいいかはぱっと見では分かりません。めちゃめちゃ大きいdの値を取ればほぼほぼ必ず定常なデータになりはしますが、それだと元のデータの情報を失いすぎてしまい、予測モデルとしての意味を失ってしまいます。
このdの最適の値を探す為に使うことができる統計学的なテクニックの一例としてAugmented Dickey–Fuller test(拡張ディッキーフラー検定)を考えることができます。コインに関する話をしているはずなので詳しいことは省きますが、この検定を行うことでdがどの段階で定常性を満たすかを推定でき、過大でも過少でもないパラメータを設定することができます。
コインの『実質貨幣学的価値』の推移データがそもそも最初から定常的であることが多く、そうでない場合でもごく小さいdの採用(つまり元のデータが持つ情報を失いすぎずに)で殆どのケースで定常となる特徴を持つことが大量のコインの分析から炙り出されたことは、分析者として非常に興味深いと感じました。
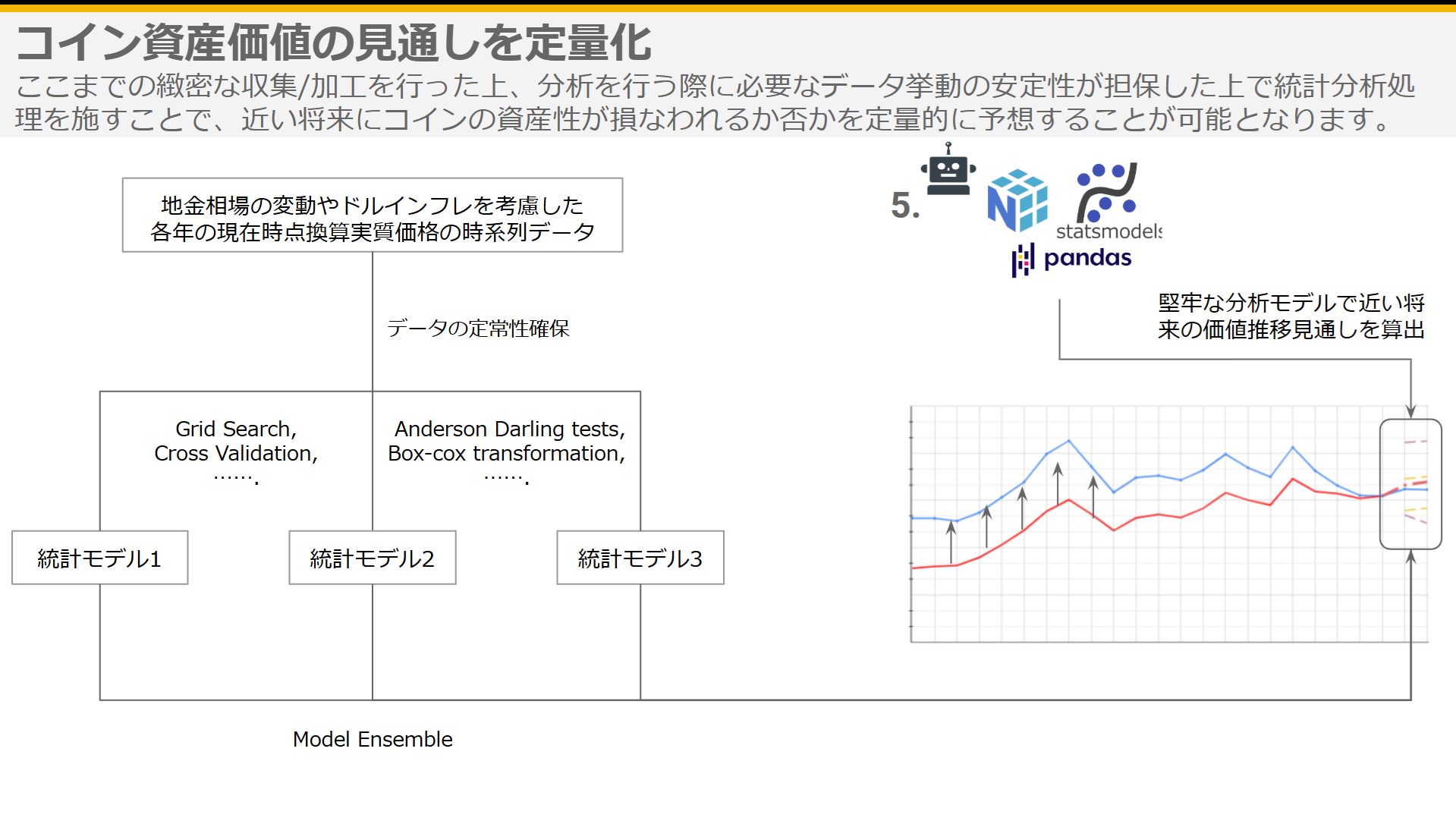
このような過不足のないdが分かれば、Grid Search, Cross Validationなど様々なテクニックを使いながら、本質を失わずにシンプル且つ堅牢なモデルを組むことができます。
上記はあくまでも一例です。
『コインに関する話をしているはずなので詳しいことは省きますが』(笑)、上記を一例として、コインの『実質貨幣学的価値』の推移データの特徴を丁寧に鑑み、相応しい加工とモデル選定をしながら3種類のモデルを組み、それらを協力させることで予測の精度を高めるためのアンサンブル学習を行うことで、分析対象のコインが近い将来、どのような資産価値の推移を辿ることが統計学的な検知から考えられるかを堅牢に推定することが可能となりました。
コインは1枚1枚愛すべき存在であり、その蒐集にこそ悦びを感じるべき営みではありますが、これを投資や資産運用の一部として考える場合、将来的にどのような資産価値の推移を辿りうるかの定量的な判断のための基準・情報は必要不可欠となってきます。
これまでコイン業界の人間が提供する様々なサービスを見てきましたが、このような側面を提供するものは『コイン定期便』のみであるかと思われます。
因みに注意していただきたい点として、私が予測を示しているのは、あくまで現在時点のドルの価値を前提としたドル建ての『実質貨幣学的価値』となります。それを近い将来の名目価格として円建てに変換した値をコイン定期便に付帯するレポートに記してはいますが、こちらドルインフレの進行・金地金価格の今後の推移に関しては過去20年の平均的な動きを加味、ドル円換算はレポート執筆時点のレートに対して上下10円分程度の幅を持たせる形で算出しています。
これらの要素の推定も行えればいいのでしょうが、それは貨幣学市場アナリストである私の仕事ではないのでご容赦いただければと思います。